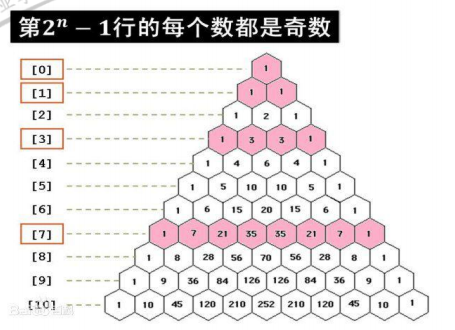
1、求杨辉三角的第m行第k个元素
第m行有m项,m是正整数,因此k一定不会大于m
第n行的m个数可表示为C(n-1, m-1),即为从n-1个不同元素中取m-1个元素的组合数
解答:
#算法1:首尾补1
m = 5
k = 4
triangle = [] #使用嵌套结构[[]]
for i in range(m):
row = [1]
triangle.append(row)
if i == 0: #第0行直接返回
continue
for j in range(1,i):
row.append(triangle[i-1][j-1] + triangle[i-1][j])
row.append(1)
print(triangle)
print(“—————-“)
print(triangle[m-1][k-1])
#算法2:组合数公式
参考:【图文】杨辉三角与组合数性质_百度文库 https://wenku.baidu.com/view/244b7925482fb4daa58d4b1d.html
#组合数公式C(m,n) = m!/(n!(m-n)!)
#m行k列的值,C(m-1,k-1)组合数
m = 9
k = 5
#c(n,r) = c(m-1,k-1) = (m-1)!/((k-1)!(m-r)!)
n = m – 1
r = k – 1
d = n – r
targets = [] #r, n-r, n
factorial = 1
for i in range(1, n+1):
factorial *= i
if i == r:
targets.append(factorial)
if i == d:
targets.append(factorial)
if i == n:
targets.append(factorial)
print(targets)
print(targets[2]//(targets[0]*targets[1]))
本文来自投稿,不代表Linux运维部落立场,如若转载,请注明出处:http://www.178linux.com/95591